◯関数の定義
\( \displaystyle x \)の値を決めると、それに対応して\( \displaystyle y \)の値がただ1つに決まるとき、\( \displaystyle y \)は\( \displaystyle x \)の関数であるという。
| 具体例 | 関係式/理由 | |
| yが\( \displaystyle x \)の関数である | 1冊120円のノート\( \displaystyle x \)冊の代金\( \displaystyle y \)円 | \( \displaystyle y = 120x \) |
| 定価\( \displaystyle x \)円の品物を3割引で買ったときの代金\( \displaystyle y \)円 | \( \displaystyle y = 0.7x \) | |
| 分速\( \displaystyle x \)mで800m進む時間\( \displaystyle y \)分 | \( \displaystyle y = \frac{800}{x} \) | |
| yが\( \displaystyle x \)の関数でない | 周囲\( \displaystyle x \)cmの長方形の面積\( \displaystyle y \)cm\( \displaystyle ^2 \) | 縦と横の組合せが複数あり、\( \displaystyle y \)が1つに決まらない |
| 身長\( \displaystyle x \)cmの人の靴のサイズ\( \displaystyle y \)cm | 身長が同じでも靴のサイズが同じとは限らない |
◯比例と反比例
| 種類 | 関係式 | 特徴 |
| 比例 | \( \displaystyle y = ax \) (\( \displaystyle a \)は比例定数) | グラフは直線 |
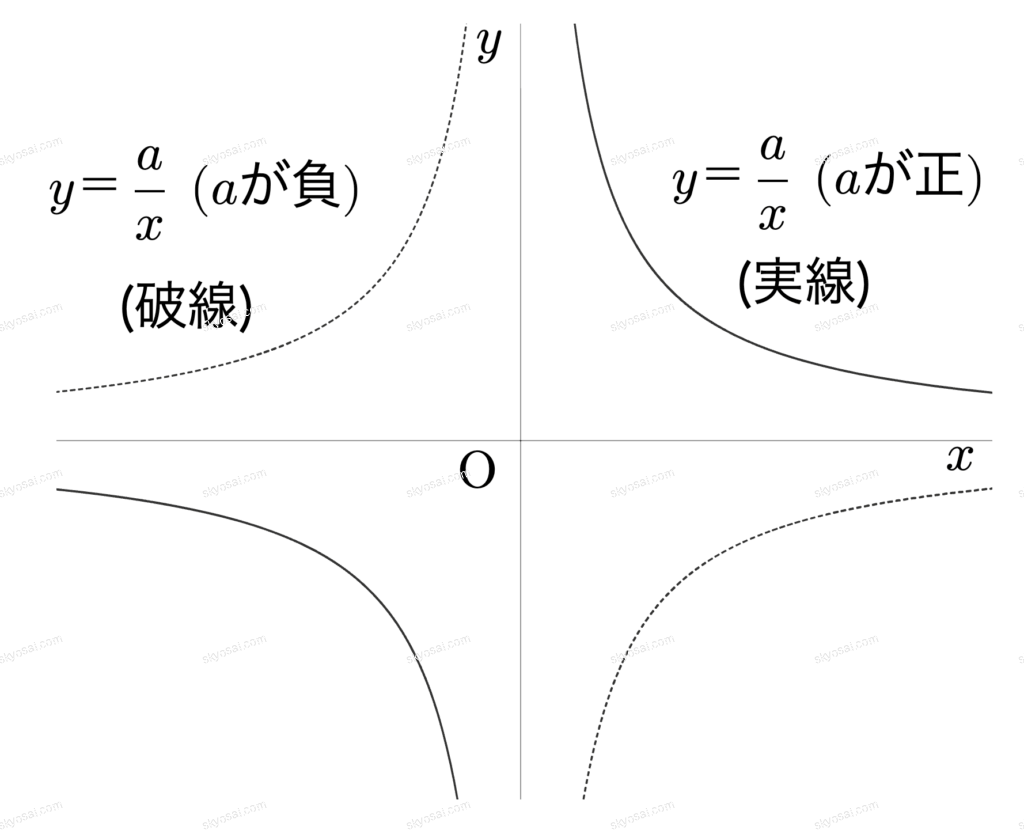
| 反比例 | \( \displaystyle y = \frac{a}{x} \) (\( \displaystyle a \)は比例定数) | \( \displaystyle xy \)の値が常に一定(\( \displaystyle a \)) |
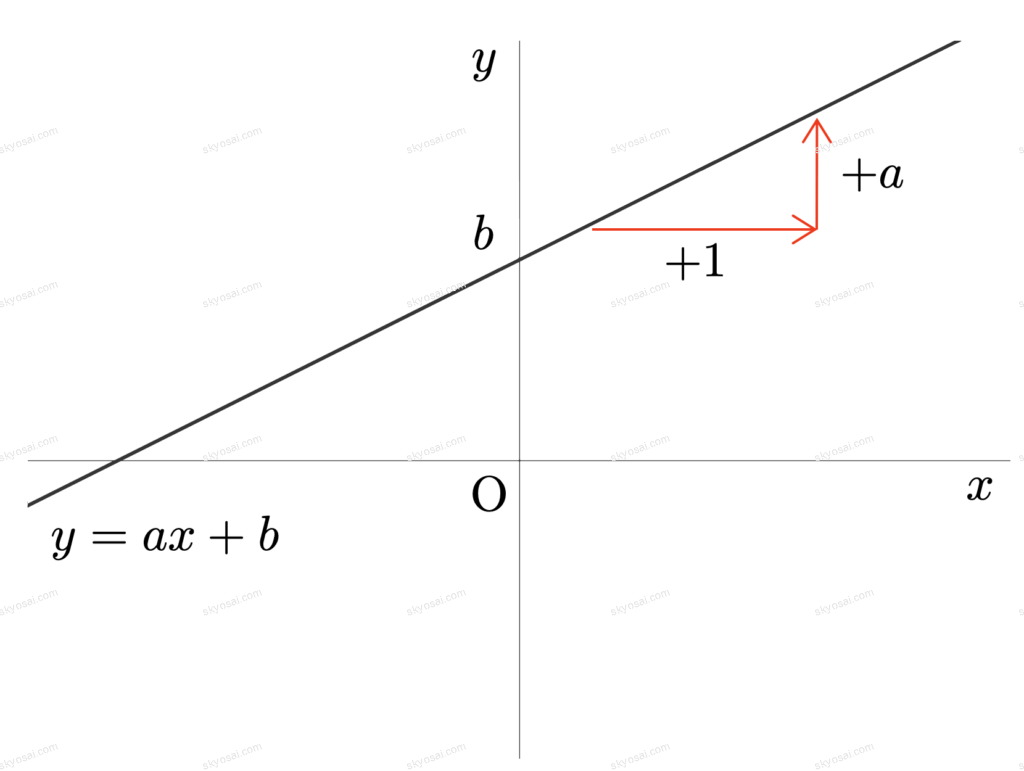
◯1次関数\( \displaystyle y=ax+b\)のグラフの性質
| 係数 | 名称 | 性質 |
| \( \displaystyle a \) | 傾き | \( \displaystyle a > 0 \) ⇒ グラフは右上がり |
| 傾き | \( \displaystyle a < 0 \) ⇒ グラフは右下がり | |
| \( \displaystyle b \) | 切片 | \( \displaystyle y \)軸との交点の\( \displaystyle y \)座標 (交点の座標は\( \displaystyle (0, b) \)) |
◯一次関数の式の決定
| 状況 | 求め方 |
| (1) 傾き\( \displaystyle a \)と通る1点\( \displaystyle (p, q) \)がわかっている | \( \displaystyle y – q = a(x – p) \)を利用する |
| (2) 通る2点\( \displaystyle (x_1, y_1), (x_2, y_2) \)がわかっている | 傾き\( \displaystyle a = \frac{y_2 – y_1}{x_2 – x_1} \)を計算後、(1)の方法で求める |
◯ \( \displaystyle y=ax^2\)のグラフの性質
| 項目 | 性質 |
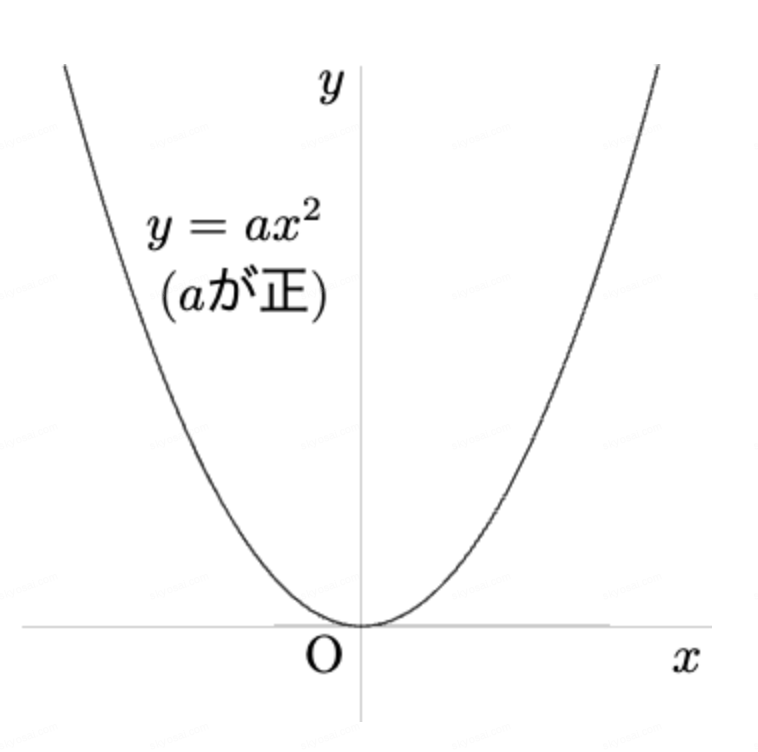
| グラフの形 | 原点\( \displaystyle (0, 0) \)を頂点とする放物線 |
| 対称軸 | \( \displaystyle y \)軸 |
| \( \displaystyle a > 0 \)のとき | 上に開いた(下に凸の)グラフ |
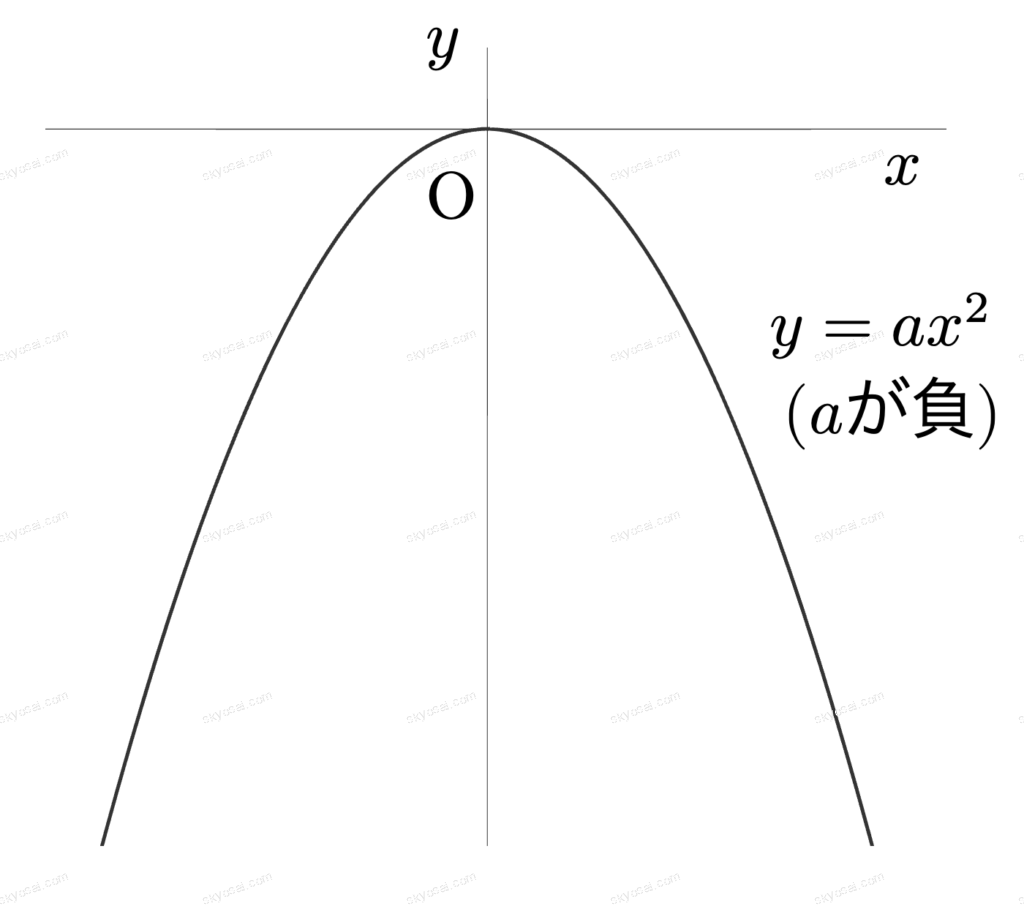
| \( \displaystyle a < 0 \)のとき | 下に開いた(上に凸の)グラフ |
◯平方完成
\( \displaystyle y = ax^2 + bx + c \) → \( \displaystyle y = a(x – p)^2 + q \)と変形することで、頂点の座標\( \displaystyle (p, q) \)と軸の方程式\( \displaystyle x = p \)がわかる。
解説ー準備中
この記事は役に立ちましたか?
間違い/不具合かな?
と思ったらこちらへ