◯確率の計算方法
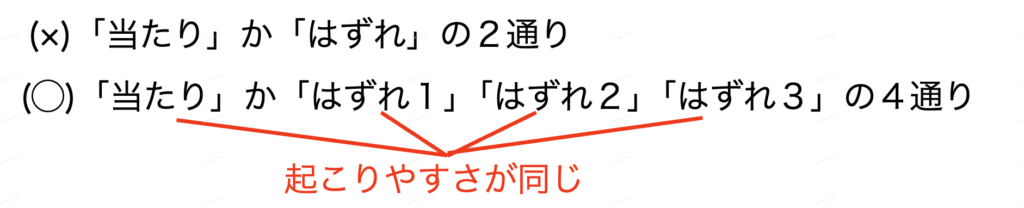
①起こりうる事柄をすべて数える。 |
※(①について)どの事柄の起こりやすさも同じになるように、同じものでも区別したり、細かく分解したりして考える。
(例)確率の計算で、当たりくじ1本、はずれくじ3本から1本ひくとき…
◯確率の性質
| 名称 | 使うとき | 計算式 |
| 加法定理 | 同時に起こらない2つの事象\( \displaystyle A, B \) (例)1または偶数の目がでる | \( \displaystyle P(A \text{ または } B) = P(A) + P(B) \) |
| 乗法定理 | 互いに独立な2つの事象\( \displaystyle A, B \) (例)硬貨とサイコロ、玉を戻して再度引く | \( \displaystyle P(A \text{ かつ } B) = P(A) \cdot P(B) \) |
◯余事象の確率
求めたい事象\( \displaystyle A\)の確率を直接計算するのが難しい場合、事象\( \displaystyle A \)が「起こらない」確率を考えることが有効なことがある。
(例)「少なくとも1本は当たり」の確率
=1- (「すべてはずれ」の確率)
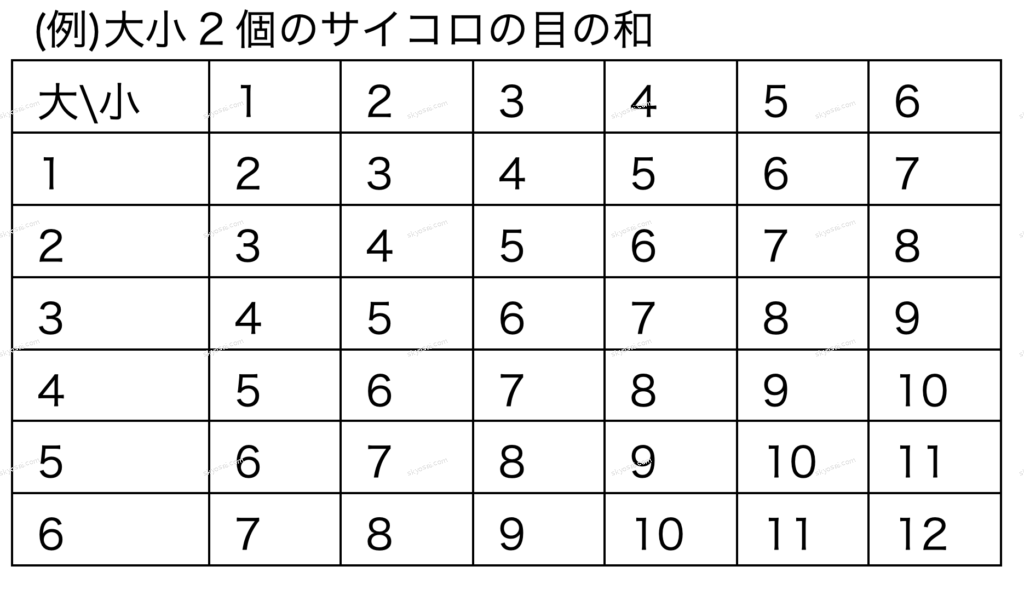
◯よくある問題1(サイコロ問題)
とくに、大小2個のサイコロを投げたときの和・差・積が問われることが多い。
下記のようにすべての場合\( \displaystyle 6 \times 6 \)を「表」に整理して、該当するものを数えて確率を計算すればよい。
◯よくある問題2(カード・くじ引き・玉を取り出す)
| 取り出し方 | 特徴 | 計算方法 |
| もとに戻す(復元抽出) | 1回ごとの試行が独立している。 | 乗法定理を使い、確率をかけ算していく。 |
| もとに戻さない(非復元抽出) | 1回ごとに全体の場合の数が減っていく。 | 順列で考えるか、確率を段階的にかけ算する(分母を減らしていく※)。 |
| 同時に取り出す | 順番を区別しない。 | 組合せ(\( \displaystyle \text{C} \))で計算する。 |
◯倍数の判定法(確率の問題でときどき使う)
| 判定法 | |
| 2の倍数 | 一の位が0, 2, 4, 6, 8 |
| 3の倍数 | 各位の数の和が3の倍数 |
| 4の倍数 | 下二桁が4の倍数 |
| 5の倍数 | 一の位が0または5 |
解説ー準備中
この記事は役に立ちましたか?
間違い/不具合かな?
と思ったらこちらへ