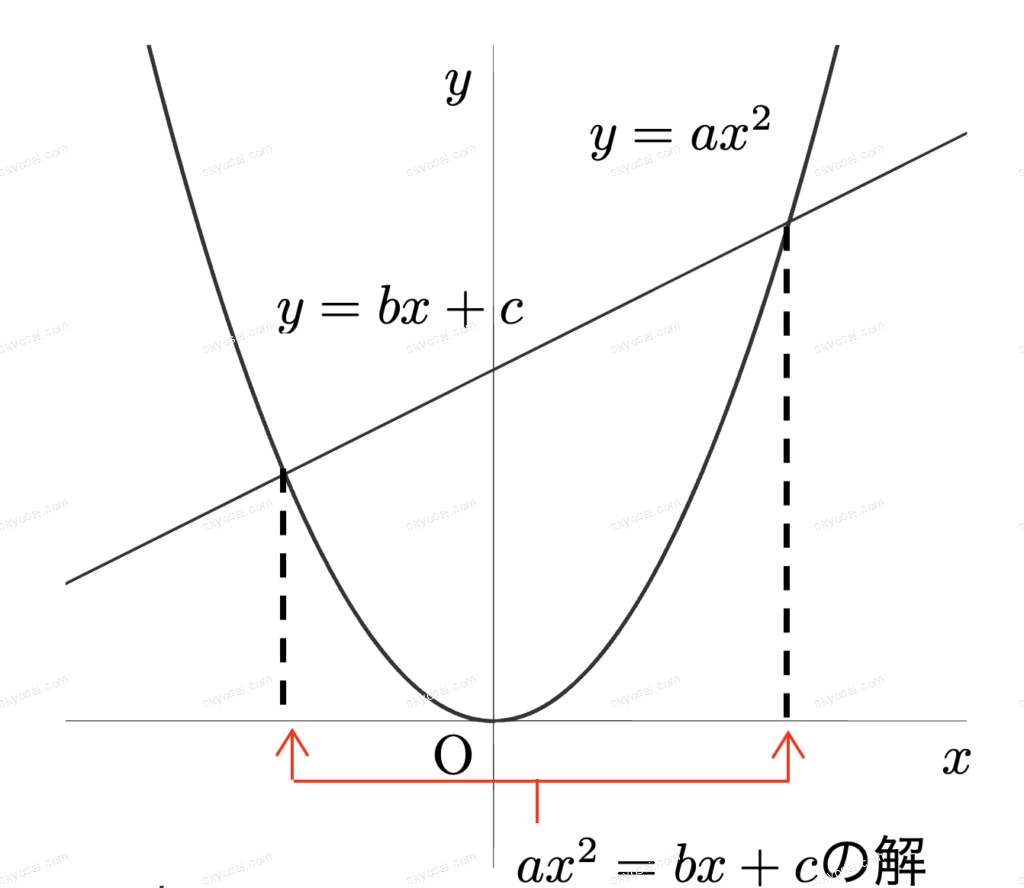
◯グラフの交点
2つの関数\( \displaystyle y = f(x) \)と\( \displaystyle y = g(x) \)の交点を調べたい
→ 連立方程式\( \displaystyle f(x) = g(x) \)を解く。解が交点の\( \displaystyle x \)座標となる。
(例)\( \displaystyle y = ax^2 \)と\( \displaystyle y = bx + c \)の交点
→ 2次方程式\( \displaystyle ax^2 = bx + c \)を解く
◯2次不等式の解法
方程式を解き、グラフの情報を使って解を求める。
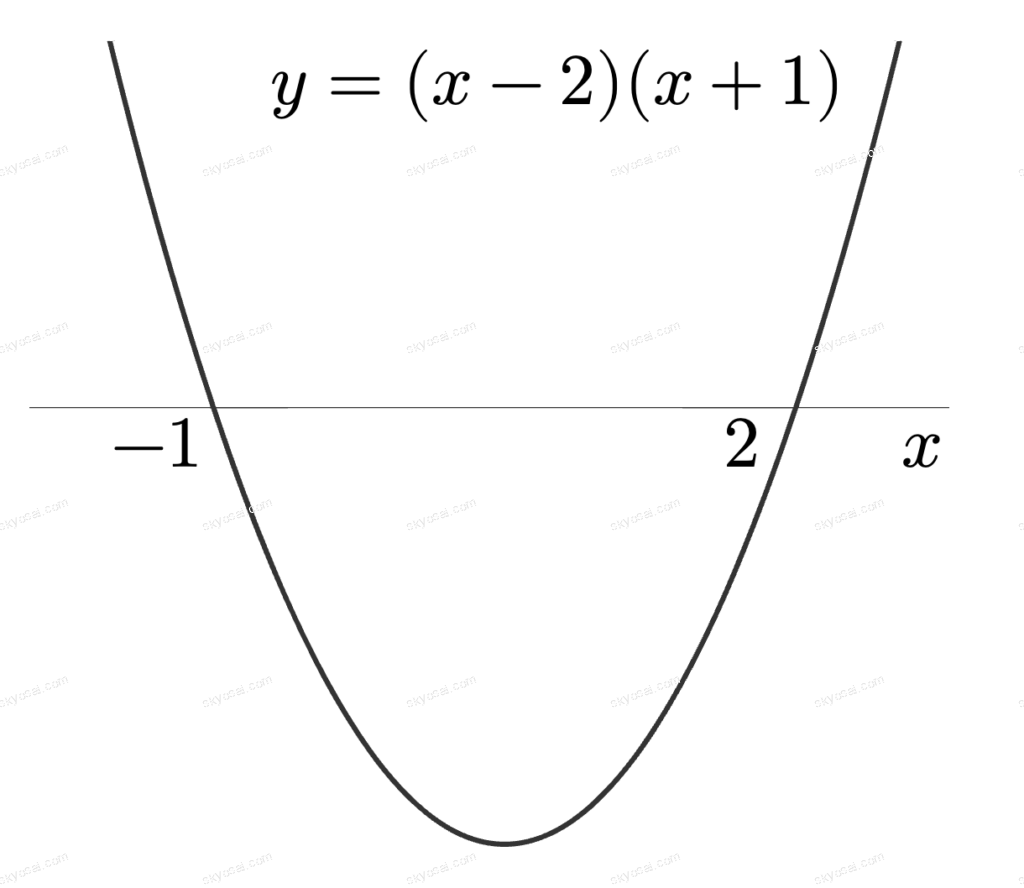
(例)\( \displaystyle x^2 – x – 2 < 0 \)
\( \displaystyle (x – 2)(x + 1) = 0 \)をとくと、\( \displaystyle x = -1, 2 \)
\( \displaystyle y = (x – 2)(x + 1) \)は下に凸の放物線
\( \displaystyle x \)軸より下にある範囲を考えて、\( \displaystyle -1 < x < 2 \)
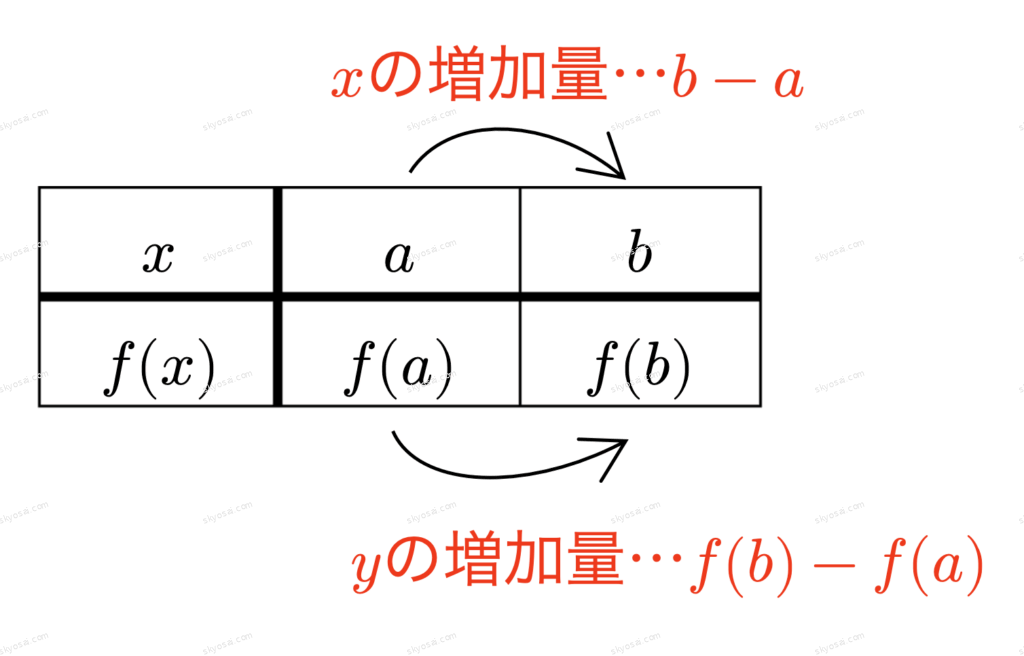
◯変化の割合
関数\( \displaystyle f(x) \)が\( \displaystyle x = a \)から\( \displaystyle x = b \)まで変化したときの
変化の割合(平均変化率)は、
\( \displaystyle \frac{yの増加量}{xの増加量} = \frac{f(b) – f(a)}{b – a} \)
◯関数の変域
…定義域(\( \displaystyle x \)の変域)に対する値域(\( \displaystyle y\)の変域)を求める。グラフを利用する。
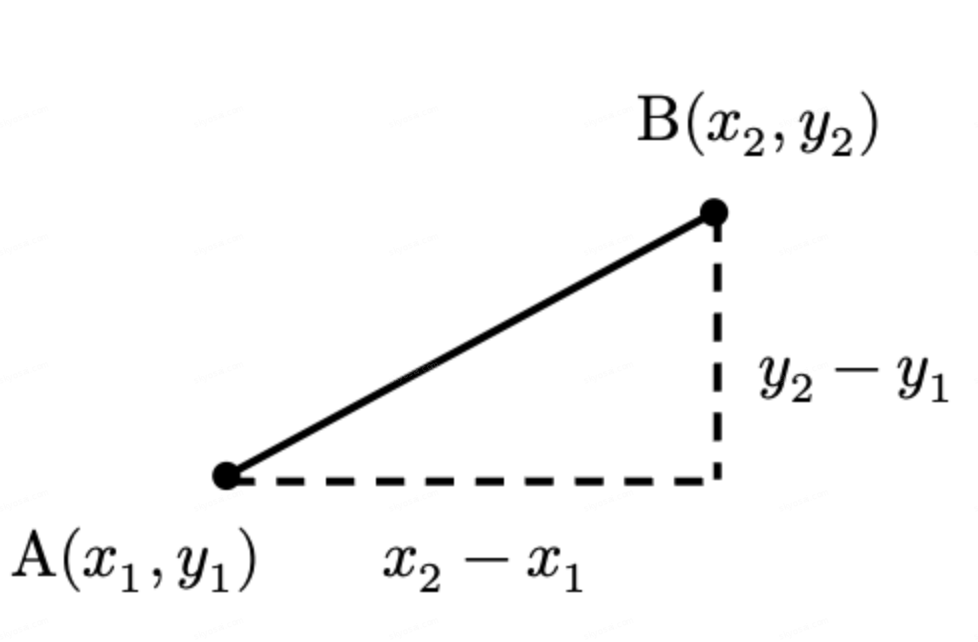
◯2点\( \displaystyle \text{A}(x_1, y_1), \text{B}(x_2, y_2) \)間の距離
| 種類 | 求め方 |
| \( \displaystyle x \)軸に平行な線分 (\( \displaystyle y_1 = y_2 \)) | \( \displaystyle |x_2 – x_1| \)の絶対値 |
| \( \displaystyle y \)軸に平行な線分 (\( \displaystyle x_1 = x_2 \)) | \( \displaystyle |y_2 – y_1| \)の絶対値 |
| 斜めの線分 | 三平方の定理を利用 \( \displaystyle \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2} \) |
◯中点の座標
2点\( \displaystyle \text{A}(x_1, y_1), \text{B}(x_2, y_2) \)を結ぶ線分の中点\( \displaystyle \text{M} \)の座標
\( \displaystyle \text{M} \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \)
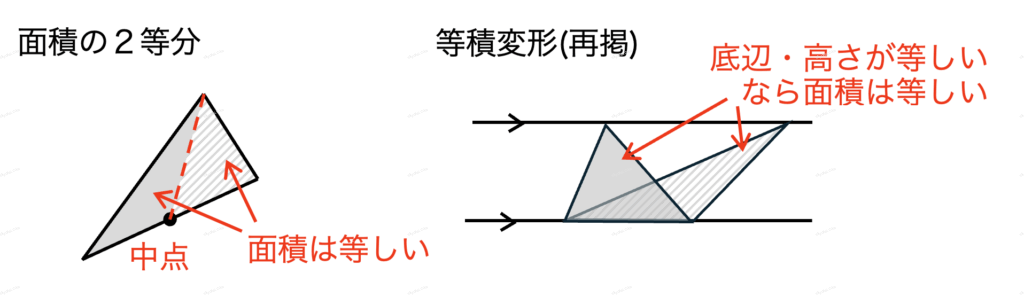
◯面積条件の処理(よく使うもの)
この記事は役に立ちましたか?
間違い/不具合かな?
と思ったらこちらへ