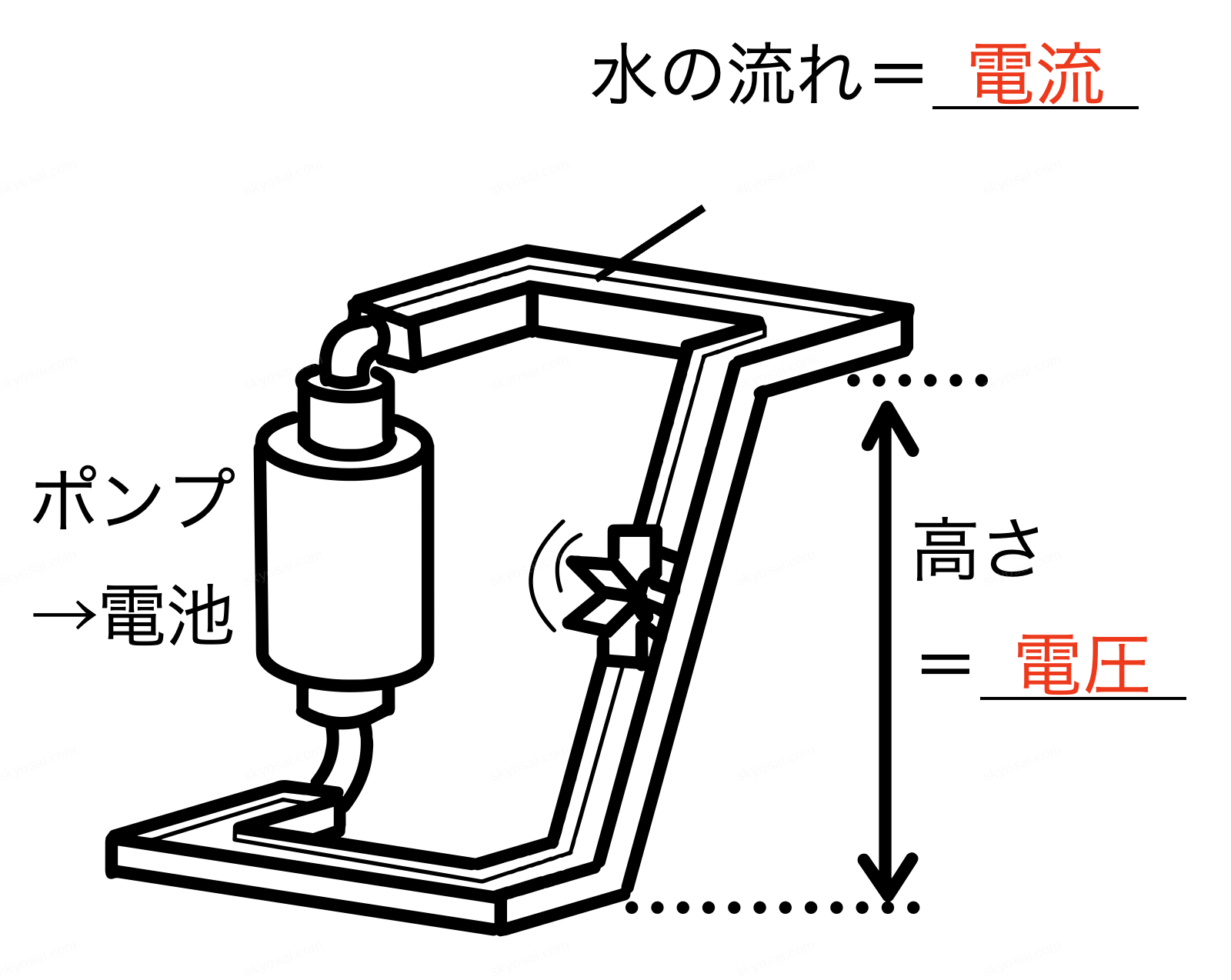
◯電流モデル(イメージの補助として活用)
| 水の例え | キーワード | |
| 電流(\( \displaystyle \text{A} \)) | 流れる水の量 (点で計測(電流計)) | 明るさ・速さ |
| 電圧(\( \displaystyle \text{V} \)) | ポンプの圧力・滝の高さ (幅で計測(電圧計)) | 押し出す力・勢い |
| 抵抗(\( \displaystyle \Omega \)) | 水車の重さ | 流れにくさ |
| 回路 | 水が巡るパイプ | 電気の通り道 |
| 乾電池 | ポンプ | 電圧をかける |
| 豆電球 | 水車 | 電流が仕事をする場所 |
◯オームの法則
ある抵抗に着目したとき、次が成り立つ。
| \( \displaystyle V [\text{V}] = I [\text{A}] \times R [\Omega] \) |
※ \( \displaystyle V, I, R \) は数字(量)で、\( \displaystyle \text{V}, \text{A}, \Omega \) は単位の意味。
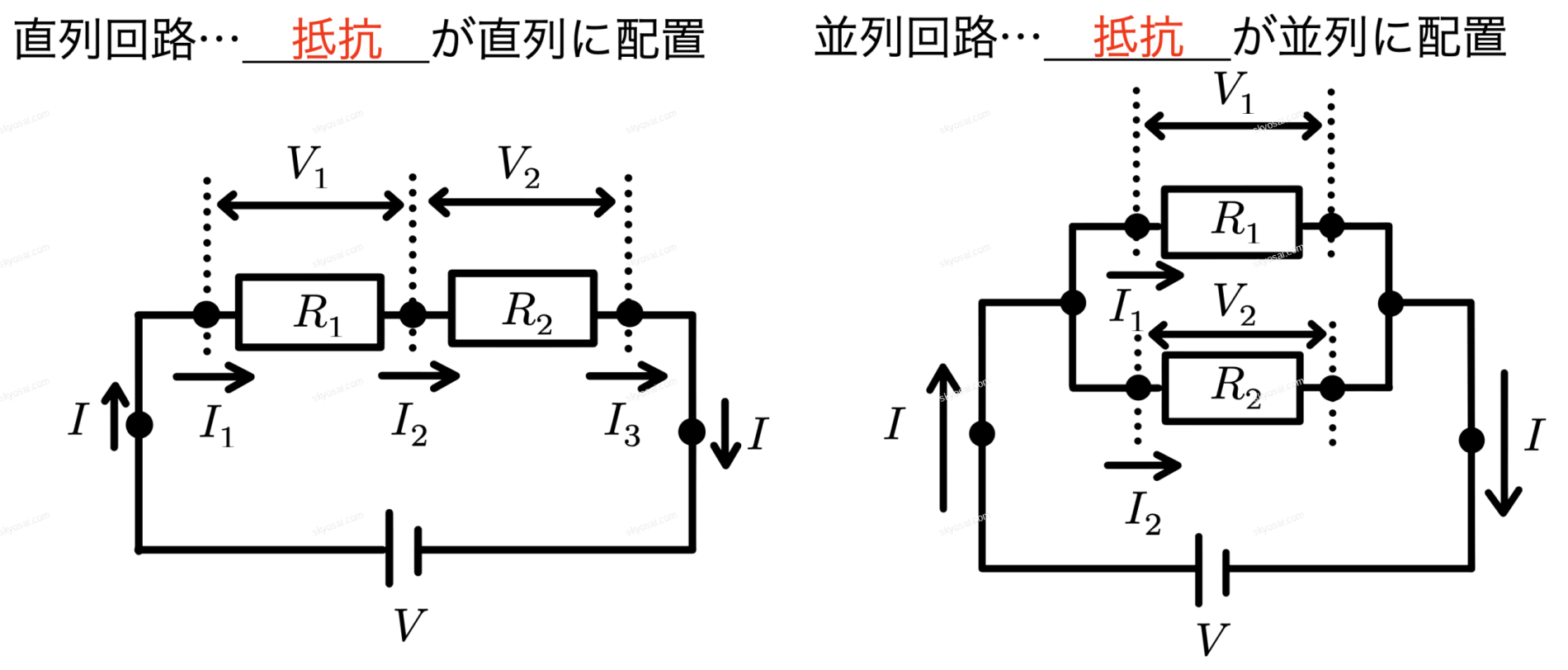
◯直列回路と並列回路の比較
| 項目 | 直列回路 | 並列回路 |
| 電流 | 回路のどの部分でも同じ大きさ \( \displaystyle I = \)\( \displaystyle I_1 = I_2 = I_3 \) | 全体の電流=各部分の電流の和 \( \displaystyle I = \)\( \displaystyle I_1 + I_2 \) |
| 電圧 | 全体の電圧=各部分の電圧の和 \( \displaystyle V = \)\( \displaystyle V_1 + V_2 \) | 各部分の電圧は電源の電圧と等しい \( \displaystyle V = \)\( \displaystyle V_1 + V_2 \) |
| 抵抗 | 全体の抵抗=各抵抗の和 \( \displaystyle R = \)\( \displaystyle R_1 + R_2 \) |
全体の抵抗の逆数=各抵抗の逆数の和
\( \displaystyle \frac{1}{R} = \)\( \displaystyle \frac{1}{R_1} + \frac{1}{R_2} \) |
◯抵抗の大きさの変化
物質の抵抗は長さに比例し、断面積に反比例する
◯電力と熱量
| 名称 | 定義 | 公式 | 単位 |
| 電力 | 電流が単位時間にする仕事の量 | \( \displaystyle 電力[W]=電圧[V]\times電流[A] \) | ワット[W] |
| 熱量 | 電熱線などから発生する熱の量 | \( \displaystyle 熱量[J]=電力[W]\times時間[s] \) | ジュール[J] |
解説ー準備中
この記事は役に立ちましたか?
間違い/不具合かな?
と思ったらこちらへ