◯速さ・時間・距離…基本公式(距離)= (速さ)×(時間)を駆使して計算。
(例1:追いつき算)
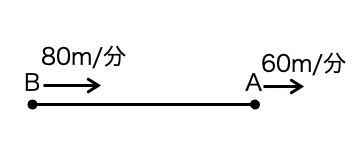
| Aが分速60mで出発した10分後に、Bが同じ地点から分速80mで追いかける。 Bが出発してからAに追いつくのは、何分後? |
・Aが先に進んだ距離は、\( \displaystyle 60 \cdot 10 = 600 \) m。
・1分間につき\( \displaystyle 80 – 60 = 20 \)m 縮まる。
→\( \displaystyle \frac{600}{20} = 30 \) だから、追いつくのは30分後。
(例2:出会い算)
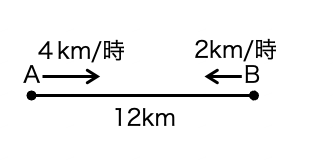
| 12km離れた地点から、Aは時速4km、Bは時速2kmで同時に向かい合って出発しました。2人が出会うのは何時間後? |
・1時間につき\( \displaystyle 4 + 2 = 6 \)km縮まる。
→\( \displaystyle \frac{12}{6} = 2 \) だから、出会うのは2時間後。
(例3:通過算(点))
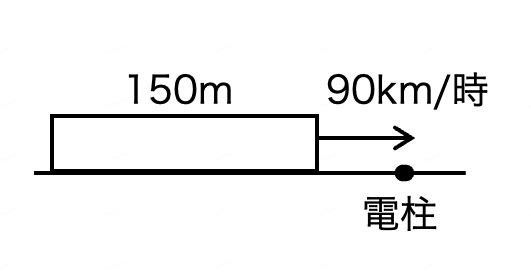
| 長さ150mの電車が、時速90kmで電柱の前を通過するのに何秒かかる? |
・時速\( \displaystyle 90 \text{km} = \) 時速\( \displaystyle 90 \cdot 1000 \text{ m} = \) 秒速 \( \displaystyle \frac{90 \cdot 1000}{60 \cdot 60} \text{m} = \) 秒速\( \displaystyle 25 \text{m} \)
・1秒間につき\( \displaystyle 25 \text{m} \)通過する。
→\( \displaystyle \frac{150}{25} = 6 \) だから、通過するのにかかるのは6秒。
(例4:通過算(トンネル))
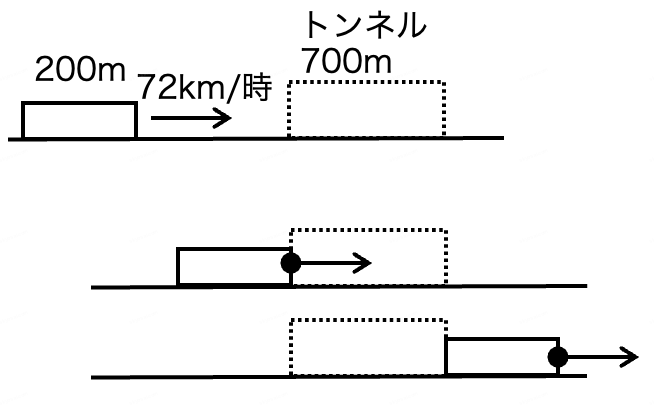
| 長さ200mの電車が時速72kmで、長さ700mのトンネルを完全に通過するのに何秒かかる? |
・時速\( \displaystyle 72 \text{km} = \) 時速\( \displaystyle 72 \cdot 1000 \text{ m} = \) 秒速 \( \displaystyle \frac{72 \cdot 1000}{60 \cdot 60} \text{m} = \) 秒速\( \displaystyle 20 \text{m} \)
・電車の最前地点が、\( \displaystyle 700 + 200 = 900 \text{ m} \)移動するのにかかる時間を求めればよい。
→\( \displaystyle \frac{900}{20} = 45 \) だから、完全に通過するのにかかるのは45秒。
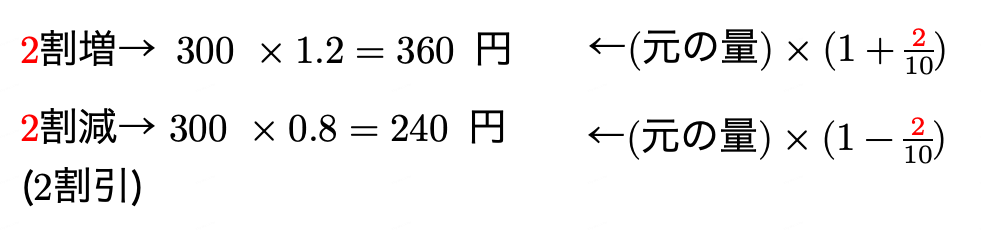
◯割合
(例)300円の商品について
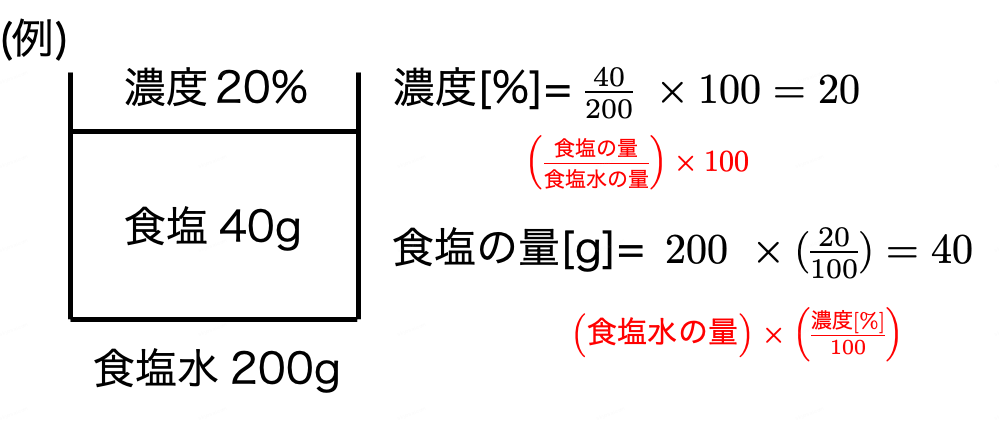
◯食塩水の濃度
食塩水を混ぜる問題は、混ぜる前と後の「食塩の量」の合計が等しいことに着目するとよい。
◯仕事算
| 考え方 | 単位時間あたりの仕事量を分数で表し、全体の仕事量を「1」として計算する。 |
| 立式例 | A管(12時間で満水)→1時間あたり\( \displaystyle \frac{1}{12} \) B管(18時間で満水)→1時間あたり\( \displaystyle \frac{1}{18} \) |
◯過不足算
| 考え方 | 配る対象の全体の個数を、異なる配り方の2通りで表現し、等式を作る。 |
| 立式例 | x人に5枚ずつ配ると4枚不足→\( \displaystyle 5x – 4 \) x人に4枚ずつ配ると12枚余る→\( \displaystyle 4x + 12 \) つまり、 \( \displaystyle 5x – 4 = 4x + 12 \)と立式できる。 |
◯比と比例式
| \( \displaystyle a : b = c : d \Leftrightarrow ad = bc \) (内側の項の積 = 外側の項の積) |
この記事は役に立ちましたか?
間違い/不具合かな?
と思ったらこちらへ